반응형
더보기
기존 부캠 때 노션에 개인적으로 정리한 것을 공부할 겸 작성한 글입니다.
개인적으로 해석해서 작성합니다. (틀릴 수 있음. 정정요청 요망ㅋ)
** 강의자료를 사용하지 않습니다 **
** 상업적 이용을 금지합니다 **
Today's Keyword
벡터, Norm, L1-norm, L2-norm, 내적, 정사영
벡터
- 공간에서 한 점. 원점으로부터 상대적 위치 표현
- 스칼라 곱 하면 길이만 변함.
- 숫자를 원소로 가지는 리스트, 배열
- 같은 모양이면 성분곱 Hadamard product
- 벡터의 덧셈 == 다른 벡터로부터 상대적 이동
Norm = 원점에서 부터의 거리

- 노름의 종류따라 다름 -> 기하학적 성질도 달라짐
- L1 norm - 변화량의 절대값 모두 더해 !
for Robust 학습, Lasso 회귀

- L2 norm - 피타고라스 정리 (a^2 + b^2 = c^2) 써서 유클리드 거리 계산해 !
for Laplace 근사, Ridge 회귀


- 두 점 사이 거리(벡터의 뺄셈) -> 제 2코사인 법칙으로 각도도 계산 가능 (각도는 L2 norm)

아 잠만 내적이요?
- 정사영(orthogonal projection)된 벡터의 길이와 관련있다.
- 정사영이 누구세요 : "곧게 쏜 그림자" (진짜임)


- 내적은 두 벡터의 Similarity를 측정하는 데 사용 가능하다
갑자기 분위기 문제 (갑분문)
Q. 두 벡터의 내적 (단일선택 , 10점)
내적이 다음과 같이 정의 될 때, 다음 두 벡터 ( xx , yy )의 내적을 구하시오.
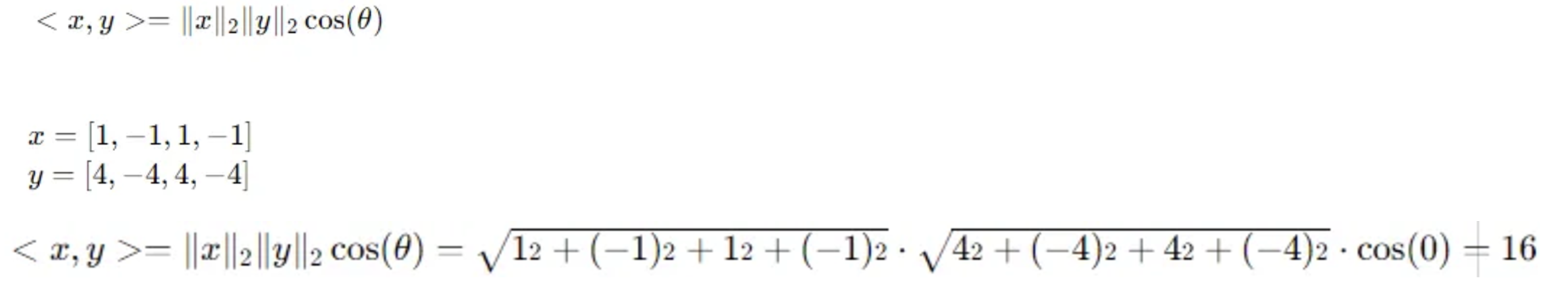
갑자기 분위기 코드 (갑분코)
import numpy as np
# 두 벡터 정의
u = np.array([3, 4])
v = np.array([4, 3])
# L1 노름 (벡터 요소의 절댓값 합)
l1_norm_u = np.sum(np.abs(u))
l1_norm_v = np.sum(np.abs(v))
# L2 노름 (벡터 크기, Euclidean Norm)
l2_norm_u = np.linalg.norm(u)
l2_norm_v = np.linalg.norm(v)
# 내적 계산
dot_product = np.dot(u, v)
# 결과 출력
print("벡터 u:", u) # 벡터 u: [3 4]
print("벡터 v:", v) # 벡터 v: [4 3]
print("\nL1 노름 (u):", l1_norm_u) # L1 노름 (u): 7
print("L1 노름 (v):", l1_norm_v) # L1 노름 (v): 7
print("\nL2 노름 (u):", l2_norm_u) # L2 노름 (u): 5.0
print("L2 노름 (v):", l2_norm_v) # L2 노름 (v): 5.0
print("\n내적 (u · v):", dot_product) # 내적 (u · v): 24
참고 : L1 norm, L2 norm, 내적 https://hwanii-with.tistory.com/5 https://m.blog.naver.com/ryumochyee-logarithm/221542210272
반응형
'AI 공부 항상하자 > 관련 이론' 카테고리의 다른 글
| [Math] Gradient Descent (착한미분맛) (1) | 2024.12.16 |
|---|---|
| [Math] 행렬을 알아보자 (1) | 2024.12.02 |

