[알고리즘/자료구조] 성공적인..어쩌구

https://inf.run/o3Vf

[무료] 성공적인 코딩 인터뷰를 위한 코딩 인터뷰 정복하기 - 코딩 테스트 - 인프런 | 강의

휘갈기며 필기해서 내 딴에 포인트라고 남긴... 다소 주관... 많이 주관적인 정리

---

Section 0 객체지향 프로그래밍 (OOP) 개념

• Class

object's data fields, methods. 뭐 함수나 데이터 정의하는 곳

• Object

class's instance 위 'fields'에 정의할 것

• Encapsulation
• Inheritance

말 그대로 상속. 코드의 재사용성을 위해서 ex) Tesla extends car

• Polymorphism

Overloading: 클래스 안 같은 이름인데 다르게 쓰일 때,
Overriding: 같은 함수인디 다른 클래스에서 쓰일 때
을 말하셨다 근데 자바 다 까먹음 ㅎㅎ;

• Abstraction

이게 살짝 이해한 게 맞는 지 모르겠으나
( 가상클래스() ) 이런 식으로 가상의 concept? 틀을 잡아주어야
다른 사람들과 코드 공유시 고유하게 사용할 수 있다 !
ex) car(start() stop()) -> Tesla (start() stop())

---

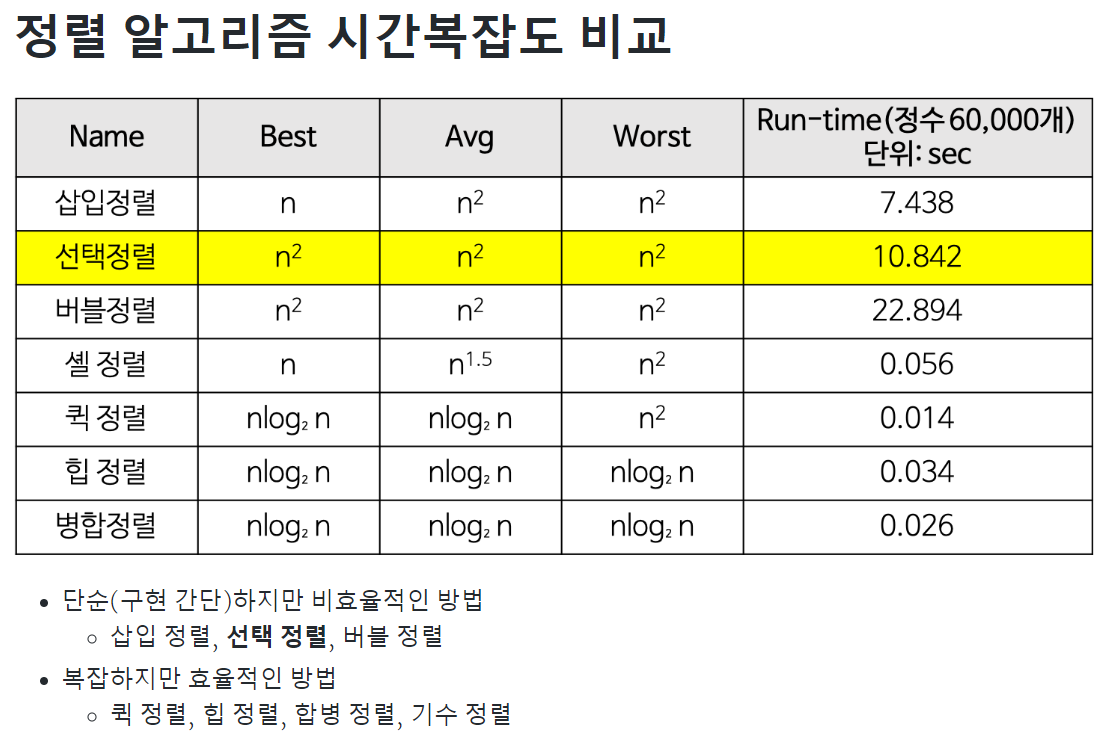
Section 1 Big-O notation 빅오표기법
분명 이것도 학교에서 배웠는데 기억이 안나버리는 마법..
코드의 효율성, 알고리즘의 performance를 표현하기 위해 사용한다.

* nO(1) = O(1) 다음과 같은 n은 알고리즘에 크게 영향주지 않는다는 것을 참고

1. O(1) : order 1 : 하나에 접근. ex) push, pop, hash
2. O(log n) : ex) Binary Search Tree Access, Search, Insertion, Deletion 이진탐색트리.. 으윽 .. n=8, log 8 = log2^3 => 3
3. O(n) : ex) traverse(순회) tree, linked list 리스트 같은 거 전체 다 돈다 !
4. O(n log n) : ex) Quick sort, Merge sort, Heap sort
5. O(n^2) : 함수안에 함수. ex) Insertion sort, Bubble sort, Selection sort

---

Section 2 Sort

sort는 아무래도 코드를 보면서 이해하는 게 편한 듯하다, 혹은 그림?
https://github.com/minsuk-heo/problemsolving/tree/master/sort

GitHub - minsuk-heo/problemsolving

https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html

• Bubble Sort

performance - O(n^2) / space complexity O(n)
인접 item swap으로 sort.
서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.
선택 정렬과 기본 개념이 유사하다.

import unittest

def bubblesort(alist):
    for i in range(len(alist)-1):
        for j in range(len(alist)-1):
            if alist[j] > alist[j+1]:
                alist[j], alist[j+1] = alist[j+1], alist[j]
    return alist


class unit_test(unittest.TestCase):
    def test(self):
        self.assertEqual([1, 2, 3, 4, 5, 6], bubblesort([4, 6, 1, 3, 5, 2]))
        self.assertEqual([1, 2, 3, 4, 5, 6], bubblesort([6, 4, 3, 1, 2, 5]))
        self.assertEqual([1, 2, 3, 4, 5, 6], bubblesort([6, 5, 4, 3, 2, 1]))

• Selection Sort

O(n^2) / minimum value 가 필요하다. 자리마다 하나씩 비교하면서 swaping
제자리 정렬(in-place sorting) 알고리즘의 하나
첫 번째 순서에는 첫 번째 위치에 가장 최솟값을 넣는다.
두 번째 순서에는 두 번째 위치에 남은 값 중에서의 최솟값을 넣는다.

import unittest

def selectionSort(input):
    for i in range(len(input) - 1):
        # assume the min is the first element
        idx_min = i
        j = i + 1

        # test against elements after i to find the smallest
        while j < len(input):
            if(input[j] < input[idx_min]):
                # found new minimum; remember its index
                idx_min = j
            j = j + 1

        if idx_min is not i:
            # swap
            input[idx_min], input[i] = input[i], input[idx_min]

    return input

class unit_test(unittest.TestCase):
    def test(self):
        self.assertEqual([1, 2, 3, 4, 5, 6], selectionSort([4, 6, 1, 3, 5, 2]))
        self.assertEqual([1, 2, 3, 4, 5, 6], selectionSort([6, 4, 3, 1, 2, 5]))
        self.assertEqual([1, 2, 3, 4, 5, 6], selectionSort([6, 5, 4, 3, 2, 1]))

• Insertion Sort

간단한데 효율성은 떨어지는.. 비교하고 옆보다 또 작으면 swap... swap...

삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
즉, 두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 세 번째, 두 번째, 첫 번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
처음 Key 값은 두 번째 자료부터 시작한다.

import unittest

def insertion_sort(input):

    for idx, valueToInsert in enumerate(input):
        # select the hole position where number is to be inserted
        holePosition = idx

        # check if previous no. is larger than value to be inserted
        while holePosition > 0 and input[holePosition-1] > valueToInsert:
            input[holePosition - 1], input[holePosition] = input[holePosition], input[holePosition-1]
            holePosition = holePosition - 1

    return input

class unit_test(unittest.TestCase):
    def test(self):
        self.assertEqual([1, 2, 3, 4, 5, 6], insertion_sort([4, 6, 1, 3, 5, 2]))
        self.assertEqual([1, 2, 3, 4, 5, 6], insertion_sort([6, 4, 3, 1, 2, 5]))
        self.assertEqual([1, 2, 3, 4, 5, 6], insertion_sort([6, 5, 4, 3, 2, 1]))

• Merge Sort

O(nlogn) / O(n) 8->4,4->2,2->1,1 완전 쪼개서 정렬하고 합쳐합쳐
이건 말보다 그림이 이해하기 편한

https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

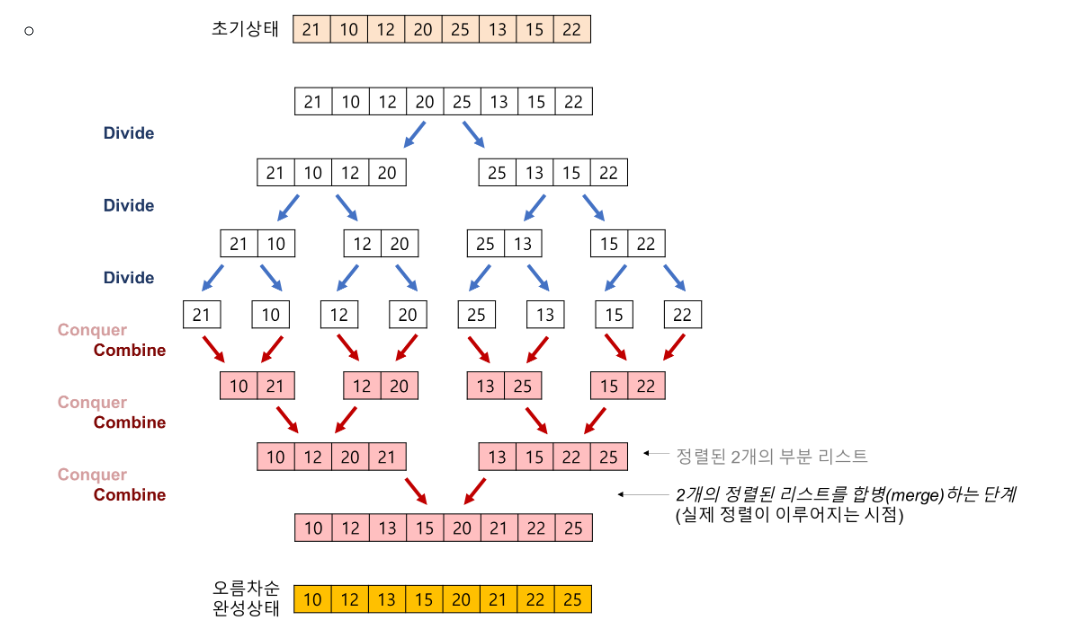
__author__ = 'Minsuk Heo'

def mergeSort(alist):
    print("Splitting ",alist)
    if len(alist)>1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i=0
        j=0
        k=0
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i < len(lefthalf):
            alist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j < len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1
    print("Merging ",alist)

alist = [6,2,4,1,3,7,5,8]
mergeSort(alist)
print(alist)

• Quick Sort

O(nlogn) (worst : O(n^2)) / O(n) 효율면에서 good
Pivot(가장 마지막을 사용)을 지정해서 비교해간다. 작으면 왼으로 이동! 크면 우로 이동! 끝났으면 pivot 다시 지정!

import unittest

def quick_sort(list, start, end):
    # repeat until sublist has one item
    # because the algorithm is using in-place space, we can not use len(list) instead we use start, end for sublist
    if start < end:
        # get pivot using partition method
        pivot = partition(list, start, end)
        # recurse quick sort left side from pivot
        quick_sort(list, start, pivot-1)
        # recurse quick sort right side from pivot
        quick_sort(list,pivot+1, end)
    return list

def partition(list, start, end):
    # use end item as initial pivot
    pivot = end
    # use start as initial wall index
    wall = start
    left = start
    # repeat until left item hit the end of list
    while left < pivot:
        # if left item is smaller than pivot, swap left item with wall and move wall to right
        # this will ensure items smaller than pivot stay left side from the wall and
        # the items greater than pivot stay right side from the wall
        if list[left] < list[pivot]:
            list[wall], list[left] = list[left], list[wall]
            wall = wall + 1
        left = left + 1
    # when left hit the end of list, swap pivot with wall
    list[wall], list[pivot] = list[pivot], list[wall]
    # now left side of wall are the items smaller than wall
    # now right side of pivot are the items greater than wall
    # wall is the new pivot
    pivot = wall
    return pivot

class unit_test(unittest.TestCase):
    def test(self):
        list = [8, 13, 2, 6, 1, 4]
        self.assertEqual([1, 2, 4, 6, 8, 13], quick_sort(list,0,len(list)-1))
        list = [8, 1, 2, 5, 10, 14, 7, 21]
        self.assertEqual([1, 2, 5, 7, 8, 10, 14, 21], quick_sort(list, 0, len(list) - 1))